Thứ Bảy, 17 tháng 11, 2018

Học thêm 2 ngôn ngữ: Toán và Lập trình trí tuệ nhân tạo

Học để thành thạo và giỏi hai ngôn ngữ “toán học” và “lập trình” chắc là rất khó. Nhưng học để biết hai ngôn ngữ này, để sẵn sàng đón nhận kỷ nguyên của AI và IoT (Vạn vật trên Internet – Internet of things), thì không quá khó. Chỉ cần bỏ thời gian và chăm chỉ học. Ngôn ngữ lập trình ngày càng gần gũi với tiếng Anh giao tiếp; còn đại số tuyến tính, là loại toán được sử dụng nhiều trong AI, thực ra cũng chỉ khó vừa vừa, bởi nó chỉ xoay quanh (và đi xa hơn một chút) các phép toán cộng, trừ, nhân, chia thông thường. Hai ngôn ngữ này có thể sẽ có vai trò quan trọng trong tương lai gần. Ai cũng nên học, nhất là những người trẻ tuổi, bởi họ sẽ phải sống phần lớn cuộc đời mình trong thế giới của AI. Rất có thể trong tương lai, mọi người thay vì nói chuyện với nhau bằng tiếng Việt, Trung, Pháp Anh … họ sẽ nói với nhau bằng ngôn ngữ lập trình. Thậm chí họ có thể còn phải nói với “máy móc”. Có thể một ngày nào đó họ sẽ quen thuộc với việc ra lệnh bằng ngôn ngữ lập trình. Buổi sáng thức dậy, họ bảo cái máy hút bụi có gắn chip AI và kết nối internet trong nhà mình: “Mày ra ngoài phố mua cho tao tờ báo giấy!”
Học thêm một ngôn ngữ!
Ngày nay có lẽ ai cũng hiểu việc biết thêm một ngôn ngữ khác tiếng mẹ đẻ của mình sẽ có ích lợi thế nào trong cuộc sống. Ngày xưa các cụ ai biết chữ Hán thì oai hơn những người xung quanh hẳn mấy bậc. Gần đây hơn là những trí thức biết tiếng Pháp, rồi tiếng Anh. Hiện nay, trong công việc và đời sống thường ngày, những ai biết các thứ tiếng, Trung, Nhật, Đức, … đều có chút lợi thế hơn những người không biết.Image result for GS Đàm Thanh SÆ¡n nhận giải Dirac
Trong thế giới số hiện nay, nơi mà xu hướng trí tuệ nhân tạo đang manh nha xuất hiện ở mọi nơi, còn nền kinh tế chuyển dần sang 4.0, rất có thể hai ngôn ngữ sau đây sẽ đóng vai trò quan trọng trong cuộc sống thường ngày. Một là ngôn ngữ toán nói chung và ngôn ngữ đại số tuyến tính nói riêng. Hai là ngôn ngữ lập trình cho trí tuệ nhân tạo, ví dụ như ngôn ngữ Python. Có nghĩa là nếu ai biết hai ngôn ngữ nói trên sẽ có thêm một chút lợi thế trong cuộc sống.
Biết hai ngôn ngữ nói trên, không có nghĩa là phải thông thạo chúng. Ta chỉ cần biết chúng ở mức đọc hiểu. Cũng giống như học ngoại ngữ, ví dụ tiếng Anh, nếu giỏi đến mức viết được tiểu luận hay hùng biện bằng tiếng Anh được thì tốt, còn không thì chỉ cần đọc hiểu là được: đọc được báo tiếng Anh, đọc phụ đề phim tiếng Anh, và cũng không nhất thiết phải hiểu 100% những gì họ viết.
*
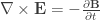
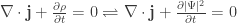
Toán là một thứ ngôn ngữ. Chỉ có điều nó không phải là ngôn ngữ tự nhiên, nó là ngôn ngữ do con người chủ ý tạo ra và được hoàn thiện dần theo thời gian.
Quãng năm 1557, có một nhà toán học xứ Wales tên là Robert Recorde. Ông này phát chán với việc làm toán mà cứ phải viết cái này bằng với cái này, ông nghĩ ra cách thay cụm từ “bằng với” bằng dấu “=”. Từ đó dấu “=” xuất hiện trong các công thức toán.
Hoặc trước đó, vào năm 1525, nhà toán học người Đức Christoph Rudolff thấy cứ phải viết chữ căn (root) của số nào đó mãi cũng chán, ông ấy biến chữ r (ký tự đầu của chữ “root”) thành dấu căn “ √ ”, và từ đó chúng ta có dấu căn trong toán học.
Ông René Descartes còn lười hơn nữa. Không chỉ nghĩ thêm từ vựng cho toán, ông ấy đặt thêm cả ngữ pháp. Khoảng năm 1637, thay vì viết phép nhân nhiều lần cùng số “x”, ví dụ “x.x.x.x” rất dài dòng và mệt, thì ông ấy viết “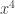x^{4}”. Descartes cũng là người quy ước dùng các số ở cuối bảng chữ cái “x,y,z” để chỉ các biến số “chưa biết, cần phải tìm”.
Ông Gottfried Leibniz thì nghĩ ra cách viết các dấu vi phân “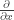\frac{\partial }{\partial x}”  và dấu tích phân “\int“. Euler thì nghĩ ra các ký hiệu nay rất quen thuộc: “e,  i, f(x), \sum”.
*
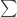Nếu ta biết tiếng Anh căn bản, ta có thể tra từ điển để đọc một tờ hướng dẫn sử dụng thiết bị được viết bằng tiếng Anh. Cũng vậy, nếu biết một chút từ vựng và ngữ pháp của toán, ta sẽ biết cách tra “từ điển” để tìm nghĩa của từ và ngữ pháp trong các công thức toán học mà ta phải tự đọc hoặc tự tìm hiểu cho công việc của mình, hoặc để mở mang kiến thức.
Ví dụ 1. Trong cơ học lượng tử, các nhà vật lý luôn quan tâm đến việc xác định vị trí và vận tốc (hay động lượng) của một hạt (ví dụ electron) trong không gian. Vị trí của hạt ở một thời điểm bất kỳ được xác định bằng các tọa độ x,y và z.
Theo kiến thức vật lý phổ thông, chúng ta ai cũng biết công thức p=m.\vec{v}(trong đó “p” là động lượng của hạt, bằng khối lượng của hạt là “m” nhân vận tốc của hạt là “\vec{v}”). Giờ giả sử chúng ta biết thêm một phép toán (toán tử) nữa, có tên gọi là toán tử giao hoán, được ký hiệu bằng dấu [x,y].
Nếu toán tử giao hoán này bằng không,  [x,y] = 0, nghĩa là hai đại lượng “x” và “y” có khả năng giao hoán. Ý nghĩa vật lý của nó là ta có thể đồng thời xác định được cả “x” và “y” (tức là ta có thể đồng thời đo được chính xác tọa độ trục x và tọa độ trục y của hạt).
Nếu toán tử giao hoán này khác không, [x,p_{x}]\neq0, nghĩa là x và p không có khả năng giao hoán. Ý nghĩa vật lý của nó là nếu ta biết (đo được) chính xác vị trí “x”, thì không thể đo được chính xác giá trị của động lượng “p”.
Nếu viết chính xác hơn, ta có:
[x,p_{x}]=i\hbar
Đây chính là Nguyên lý bất định Heisenberg. Nguyên lý này phát biểu bằng lời như sau:  “Ta không thể đồng thời xác định chính xác được cả vị trí lẫn vận tốc (xung lượng) của một hạt. Nếu ta biết càng chính xác đại lượng này, thì ta biết kém chính xác đại lượng kia”. Nếu phát biểu bằng  toán học, nguyên lý này được viết ngắn gọn như sau:
\bigtriangleup x.\bigtriangleup p_{x}> \frac{\hbar}{2}
 *
Ví dụ 2. Giả sử ta quên hết kiến thức toán, và cũng không hiểu gì về hàm sóng trong cơ lượng tử; nhưng ta vẫn nhớ một quy tắc cơ bản của ngữ pháp trong ngôn ngữ toán học: cần chặt chẽ và logic trong suy luận. Giờ chúng ta cùng nhìn vào phương trình sóng của Schrödinger:
i\hbar\frac{\partial \Psi}{\partial t}= \widehat{H}\Psi
Vế phải có {\Psi} là hàm sóng.
Ta được cho biết thêm, cùng bên vế phải của phương trình có  \widehat{H} (đọc là toán tử năng lượng Hamilton) là một số thực. Còn vế trái của phương trình có:  \hbar (hằng số Planck rút gọn) là số thực, i là số ảo (i^{2} =-1).
Từ đây ta có thể suy luận như sau: nếu ở vế trái, có \Psi  mà là số thực, thì hai vế của phương trình sẽ mâu thuẫn nhau, kết quả của vế phải là số thực, kết quả của vế trái là số phức (do có chứa thành phần là số ảo i). Để không mâu thuẫn, hàm sóng \Psi  buộc phải là số phức. (Đây là cách chứng minh phản chứng quen thuộc trong toán phổ thông.)
Nhưng hàm sóng mà là số phức (có thành phần là số ảo i), thì không thể đo lường bằng thực nghiệm (mọi đại lượng muốn đo lường được thì phải là số thực).
Chính tác giả của phương trình sóng nói trên, nhà vật lý Schrödinger, cũng bí và không biết giải thích hàm sóng này là gì. Sau đó nhà vật lý Max Born mới đề xuất một ý tưởng, ông lấy bình phương hàm sóng, \left | \Psi \right |^{2}, và sau khi bình phương nó  trở thành số thực, và tỷ lệ với xác suất tìm thấy một hạt ở một điểm cho trước trong không gian (xác suất là một đại lượng ta có thể đo được). Đề xuất này góp phần mang đến cho Max Born một giải Nobel Vật lý.  (Born và học trò của mình là Jordan đã góp công hoàn thiện phiên bản Heisenberg của cơ lượng tử, có tên gọi là cơ học ma trận, vào năm 1925. Năm 1927 Heisenberg đưa ra nguyên lý bất định và đến năm 1932/1934 được giải Nobel. Born được Einstein đề cử Nobel cùng năm với Heisenberg, nhưng đến năm 1954 mới được giải, còn Jordan thì không.)
*
Trong Ví dụ 2 ta thấy một khái niệm rất khó hiểu trong vật lý lượng tử, rất khó diễn đạt bằng lời, nhưng khi diễn đạt bằng ngôn ngữ toán học lại dễ hiểu, ngắn gọn và chính xác. Ngay cả khi ta quên gần hết kiến thức toán, chỉ nhìn vào công thức và được giải thích thêm một chút là ta hiểu.
Nói rộng ra, nếu ta biết từ vựng và quy tắc ngữ pháp của toán, ta sẽ dễ dàng đọc hiểu những gì người khác diễn đạt bằng ngôn ngữ toán:
Ví dụ 3: Nhìn vào phương trình (x – a)2 + (y – b)2 = R2 ta sẽ hiểu ngay đây phương trình biểu diễn một đường tròn trên mặt phẳng, trong hệ tọa độ hai trục x và y. Đường tròn này có bán kính R và  tâm là điểm có tọa độ trên trục x là “a” và trục y là “b”.
Ví dụ 4: Đây là phương trình Fisher: 1+i=(1+r)(1+\pi ^{e}). Trong đó i là lãi suất danh nghĩa, r là lãi suất thực, \pi ^{e} là lạm phát kỳ vọng. Để đơn giản hóa, người ta tính xấp xỉ phương trình này: {r=i-\pi ^{e}}. Tức là nếu ta muốn biết lãi suất thực mà ngân hàng trả cho các khoản tiền gửi tiết kiệm, ta chỉ cần lấy lãi suất danh nghĩa (tức lãi suất ngân hàng công bố) trừ đi lạm phát.
*
Ngôn ngữ toán học cũng chính là ngôn ngữ mà trí tuệ nhân tạo (AI) giao tiếp với thế giới bên ngoài để  tự học hỏi và dần trở nên hiểu biết và thông minh hơn. Nó dùng ngôn ngữ toán để tiếp thu thông tin từ thế giới xung quanh (thông qua các cảm biến và camera) và từ dữ liệu trên internet.
Tên gọi “trí tuệ nhân tạo” tự nó đã có nghĩa là một loại “trí tuệ” do con người tạo ra. Con người tạo ra trí tuệ ấy bằng cách lập trình. Để lập trình được, họ dùng “ngôn ngữ lập trình”, là một ngôn ngữ cũng do con người tạo ra để nói chuyện với máy móc. Ngôn ngữ lập trình cũng có sự tiến hóa riêng của nó, và càng ngày nó càng giống ngôn ngữ tự nhiên của chúng ta, cụ thể là nó rất giống tiếng Anh giao tiếp.
Ví dụ 5. Giả sử ta muốn bảo “máy” tính tổng của hai số bất kỳ (do ta tùy ý nhập vào máy). Phần Source Code thể hiện các dòng lệnh “input” cho phép ta nhập số liệu và hiển thị câu chỉ dẫn để nhập liệu “Enter first number”. Phần Output thể hiện chương trình khi được “run” (có nghĩa là “chạy” chương trình). Trong ví dụ này, người chạy chương trình nhập số thứ nhất (number 1) là 1.5 và số thứ hai (number 2) là 6.3. Kết quả cho biết tổng (sum) là 7.8.
Nếu đọc từng dòng lệnh, ta thấy ngôn ngữ lập trình dùng để điều khiển máy tính không khác gì ngôn ngữ (ở đây là tiếng Anh) được sử dụng hằng ngày.
Vi du 5
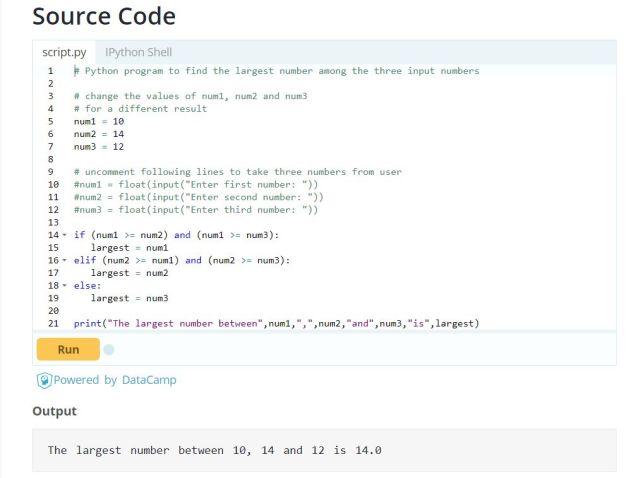
Ví dụ 6: Giả sử ta muốn lập một chương trình mà ta có thể nhập vào ba con số rồi bắt chương trình ấy tìm ra số lớn nhất. Đọc kỹ từng dòng lệnh, ta sẽ thấy phần so sánh các con số sử dụng ngôn ngữ rất gần gũi với con người: nếu (if) và (and) thì (elif), còn nếu không thì (else). Phần kết quả (ouput) cho ta biết số lớn nhất trong ba con số được nhập vào.
Vi du 6
(Hai ví dụ về lập trình ở trên là ví dụ của trang dạy lập trình Programiz, cả hai ví dụ này đều sử dụng ngôn ngữ lập trình Python.)
*
Học để thành thạo và giỏi hai ngôn ngữ “toán học” và “lập trình” chắc là rất khó. Nhưng học để biết hai ngôn ngữ này, để sẵn sàng đón nhận kỷ nguyên của AI và IoT (Vạn vật trên Internet – Internet of things), thì không quá khó. Chỉ cần bỏ thời gian và chăm chỉ học. Ngôn ngữ lập trình ngày càng gần gũi với tiếng Anh giao tiếp; còn đại số tuyến tính, là loại toán được sử dụng nhiều trong AI, thực ra cũng chỉ khó vừa vừa, bởi nó chỉ xoay quanh (và đi xa hơn một chút) các phép toán cộng, trừ, nhân, chia thông thường.
Nói cách khác, hai ngôn ngữ này có thể sẽ có vai trò quan trọng trong tương lai gần. Ai cũng nên học, nhất là những người trẻ tuổi, bởi họ sẽ phải sống phần lớn cuộc đời mình trong thế giới của AI. Rất có thể trong tương lai, mọi người thay vì nói chuyện với nhau bằng tiếng Việt, Trung, Pháp Anh … họ sẽ nói với nhau bằng ngôn ngữ lập trình. Thậm chí họ có thể còn phải nói với “máy móc”.
Có thể một ngày nào đó họ sẽ quen thuộc với việc ra lệnh bằng ngôn ngữ lập trình. Buổi sáng thức dậy, họ bảo cái máy hút bụi có gắn chip AI và kết nối internet trong nhà mình: “Mày ra ngoài phố mua cho tao tờ báo giấy!”
*
Hai nhà vật lý hàng đầu thế kỷ 20 là Einstein và Dirac cũng đóng góp rất nhiều vào từ vựng và ngữ pháp của toán. Vì lười nên Einstein gét cách viết tổng \sum_{\i=1 }^{3}=c_{i}x^{i}=c_{1}x^{1}+c_{2}x^{2}+c_{3}x^{3}. Ông viết ngắn gọn: y=c_{i}x^{i}, trong đó i không phải là lũy thừa bậc i, mà là chỉ số trên hoặc dưới, cứ có 2 chỉ số thế này, nghĩa là phép tổng với i chạy từ 1 đến 3. Trong phương trình trường của Thuyết tương đối, i chạy từ 0 đến 4.
Tích Cik của ma trận Aij  (i hàng, j cột) với ma trận cột Bjk (j hàng, k cột) nhìn phức tạp thế này:
\mathbf {C} _{ik}=(\mathbf {A} \mathbf {B} )_{ik}=\sum _{j=1}^{N}A_{ij}B_{jk}
nhưng nếu dùng cách viết tổng của Einstein sẽ chỉ còn ngắn gọn thế này: {C^{i}{}_{k}=A^{i}{}_{j}B^{j}{}_{k}}
Dirac thì nghĩ ra ký hiệu Bra-Ket. Vector Ket, \left|\Psi\right\rangle, là vector trạng thái, thực chất là ma trận cột. Vector Bra, \left\langle\Phi\right|, bản chất là số phức liên hợp của Ket, và là ma trận hàng.
Nhờ các cách viết của Einstein và Dirac mà các phép tính nhân ma trận (và cũng là nhân vector) trở nên gọn gàng đơn giản. Phương trình Einstein (thuyết tương đối) và phương trình Schrödinger (hàm sóng) có dạng ngắn gọn như sau:
Phương trình Einstein:
R_{\mu \nu} - {1 \over 2}g_{\mu \nu}\,R + g_{\mu \nu} \Lambda = {8 \pi G \over c^4} T_{\mu \nu}
Phương trình Schrödinger:
i\hbar {\frac {\partial }{\partial t}}|\psi (t)\rangle ={\hat {H}}|\psi (t)\rangle
Mọi người có thể so sánh với cách viết bình thường phương trình Schrödinger cho hạt trong hệ tọa độ 3 chiều:
i\hbar\frac{\partial}{\partial t} \Psi(\mathbf{r},\,t) = -\frac{\hbar^2}{2m}\nabla^2 \Psi(\mathbf{r},\,t) + V(\mathbf{r})\Psi(\mathbf{r},\,t)
Trong phương trình trên, ta thấy ký hiệu {\nabla^2} (napla bình phương). Đây cũng là một “cú pháp” do ông Laplace người Pháp nghĩ ra (chắc cũng vì lười). Bởi vậy nó có tên là toán tử vi phân Laplace. Thay vì viết “tổng các đạo hàm bậc hai theo 3 trục tọa độ x, y, z: \Delta f=\sum _{i=1}^{n}{\frac {\partial ^{2}f}{\partial x_{i}^{2}}} “, ta có thể viết ngắn gọn thế này: “{\nabla^2f}” là xong.
Ví dụ cuối cùng:
Sau khi biết ký hiệu hình tam giác ngược {\nabla} (đọc là nabla), là ký hiệu đạo hàm theo ba trục tọa độ, ta có thể liên hệ với mật độ điện tích (ρ) và mật độ dòng (j) do Benjamin Franklin đặt ra mà ta đã biết trong bài Pháp Quyền và Pháp Trị. Phương trình bảo toàn điện tích như sau:
{{\frac {\partial \rho }{\partial t}}+\nabla \cdot \mathbf {j} =0}
Diễn đạt bằng lời như sau: tốc độ biến thiên theo thời gian của mật độ diện tích (đạo hàm theo thời gian t) được bù trừ bằng tốc độ biến thiên của mật độ dòng theo không gian (đạo hàm theo các trục tọa độ).
Điều thú vị là dạng phương trình bảo toàn này là giống nhau ở rất nhiều lý thuyết vật lý, từ cơ học chất lưu, nhiệt học, đến lý thuyết trường cổ điển (Maxwell) và lý thuyết trường lượng tử (quantum field theory).
Trong phương trình Maxwell-Faraday đây, ta thấy biến thiên điện trường (E) trong không gian bằng với biến thiên từ trường (B) theo thời gian, và ngược lại. Đây là cái mà ta rất quen thuộc trong vật lý phổ thông, và giống giống với nguyên lý của máy phát điện (và động cơ điện).
\nabla \times \mathbf {E} =-{\frac {\partial \mathbf {B} }{\partial t}}
Còn viết dưới dạng hàm sóng, phương trình Maxwell có dạng phương trình vi phân bậc hai, nhìn như thế này (c là vận tốc ánh sáng trong chân không):
{\begin{aligned}{\frac {1}{c^{2}}}{\frac {\partial ^{2}\mathbf {E} }{\partial t^{2}}}-\nabla ^{2}\mathbf {E} =0\\{\frac {1}{c^{2}}}{\frac {\partial ^{2}\mathbf {B} }{\partial t^{2}}}-\nabla ^{2}\mathbf {B} =0\end{aligned}}
Còn trong cơ lượng tử,  ρ sẽ là mật độ xác suất (mà ta vừa biết ở trên là do Max Born nghĩ ra), còn j là mật độ dòng xác suất.
  {\nabla \cdot \mathbf {j} +{\frac {\partial \rho }{\partial t}}=0\rightleftharpoons \nabla \cdot \mathbf {j} +{\frac {\partial |\Psi |^{2}}{\partial t}}=0}
*
Một phần của bài viết trên đã đăng trên TTCT (tuần báo), số ra tuần này. Và cũng để câu thêm view cho Bầu trời chiều ẩn giấu.
Còn bài viết dưới đây là về sự kiện anh Đàm Thanh Sơn được giải Dirac, bài cũng đã đăng trên TT (nhật báo) số ra ngày hôm nay. Báo TT ngày hôm nay này dành 2 trang đăng các bài viết về anh Sơn, có bài của anh Ái Việt nữa.
Image result for GS Đàm Thanh Sơn nhận giải Dirac
GS Đàm Thanh Sơn nhận giải Dirac
Giải thưởng Dirac 2018 (Dirac Medal 2018) mới được trao cho ba nhà vật lý lý thuyết xuất sắc Subir Sachdev (Đại học Harvard), Đàm Thanh Sơn (Đại học Chicago) và Xiao-Gang Wen (Học viện công nghê Massachusetts – MIT)— vì các nghiên cứu độc lập của ba nhà vật lý này đã góp phần mang đến những hiểu biết sâu sắc và mới mẻ cho vật lý lý thuyết. Các nghiên cứu của ba nhà vật lý nhận giải Dirac năm nay đã đưa ra các kỹ thuật mới và độc đáo trong hệ đa –thể (many-body system).
Các nghiên cứu của ba nhà vật lý nói trên liên quan đến các hiệu ứng của cơ học lượng tử tác động lên hệ đa thể quy mô lớn (hệ đa-thể là một nhóm các hạt vi mô).
Trong cuộc sống thường ngày chúng ta quen thuộc với ba dạng (pha) của vật chất là rắn, lỏng, khí. Tuy nhiên trong vật lý lượng tử hiện đại, khi ta thay đổi thật chậm các tham số bên ngoài như nhiệt độ và áp suất, vật chất sẽ “chuyển pha” và do đó đột sinh các đặc tính mới.
Các nhà vật lý từ lâu đã có hiểu biết sâu sắc về việc các định luật của cơ học lượng tử tác động lên một nhóm nhỏ các hạt. Nhưng như chúng ta cũng biết, các đối tượng vật chất thường ngày chứa các nhóm hạt vi mô có số lượng cực kỳ lớn. Số lượng hạt trong nhóm là rất lớn, ngay cả so với trí tưởng tượng thông thường gần tới 1023 (một con số có tới 23 con số 0 đứng sau, nếu ta so với số đếm là tỷ, chỉ có 9 con số 0 đứng sau). Trong một hệ có hằng hà vô số hạt vi mô như vậy, sẽ có vô vàn cách thức để các hạt tương tác với nhau. Hệ quả là để áp dụng cơ học lượng tử lên hệ đa-thể này là cực kỳ phức tạp về mặt toán học.
Chìa khóa để hiểu các đặc tính của hệ đa-thể là phải sử dụng hình thái toán học số phức của liên đới lượng tử (quantum entanglement) để tìm hiểu các đặc tính của vật chất. Các công trình của ba nhà vật lý Đàm Thanh Sơn, Subir Sachdev, Xiao-Gang Wen đã đóng góp những ý tưởng và phương pháp cực kỳ mới mẻ giúp làm sáng tỏ các hình thái của liên đới lượng tử electron có thể tạo ra các đặc tính mới của vật chất như thế nào.
Những hiểu biết mới về tính chất vật lý của hệ đa-thể, nhờ vào công trình của ba nhà vật lý được giải Dirac năm nay, sẽ giúp thế giới khoa học hiểu được các đặc tính khác nhau của vật liệu, từ đó có thể thiết kế các vật liệu mới dùng trong các ứng dụng như các thiết bị siêu dẫn hay tính toán lượng tử.
Giáo sư Đàm Thanh Sơn là cựu học sinh Chuyên toán Đại học tổng hợp Hà Nội. Anh đoạt huy chương vàng toán quốc tế (IMO) với số điểm tuyệt đối 42/42 năm 1984 khi mới 15 tuổi.
Giáo sư Đàm Thanh Sơn là nhà vật lý lý thuyết đầu tiên sử dụng các hiểu biết vật lý của đối ngẫu trường chuẩn/trọng trường (gauge/gravity duality) để nghiên cứu các vấn đề tương tác trong hệ đa-thể, từ pha của nhiệt độ cực thấp là các hạt nguyên tử bị bẫy đông lạnh (cold trapped atom) đến pha của nhiệt độ cực cao là plasma của các hạt quark-gluon.
Giáo sư Đàm Thanh Sơn có những công trình quan trọng giúp thúc đẩy sự phát triển sự hiểu biết của lý thuyết trường chuẩn (gauge theory). Đây là  một lý thuyết rất quan trọng trong vật lý hiện đại. Công trình của Giáo sư Đàm Thanh Sơn liên quan đến Thống kê Fermi-Dirac và Phương trình Dirac (một trong những phương trình được bình chọn là đẹp nhất của vật lý lý thuyết, vì phương trình này tiên đoán được hạt “phản vật chất” và là phương trình đầu tiên kết hợp được lý thuyết cơ học lượng tử là Thuyết tương đối hẹp của Einstein.)
Các lĩnh vực nghiên cứu của Giáo sư Đàm Thanh Sơn bao gồm: Lý thuyết dây, Vật lý hạt nhân, Vật lý vật chất mật độ cao, Vật lý nguyên tử.
Công trình được giải Dirac năm nay của Giáo sư Đàm Thanh Sơn nằm trong lĩnh vực Vật lý nguyên tử.
Giáo sư Đàm Thanh Sơn là viện sĩ Viện Hàn lâm Khoa học tự nhiên và Khoa học Xã hội Hoa Kỳ (American Academy of Arts & Sciences), và viện sĩ Viện Hàn lâm Khoa học quốc gia Hoa Kỳ (National Academy of Sciences ).
Giải thưởng Dirac được trao hằng năm vào ngày 8 tháng 8, là ngày sinh của Dirac.
https://5xublog.wordpress.com/2018/08/10/hoc-them-mot-ngon-ngu/#more-5353
Người đăng: vào lúc

Không có nhận xét nào:

Đăng nhận xét

Đăng ký: Đăng Nhận xét (Atom)